Теорема о раскраске множества в два цвета

Раскраска двудольного графа в два цвета
На втором курсе университета учебный год нам объявили что пора уже задумываться о выборе научного руководителя, поскольку зима третий курс близко. Как раз в том учебном году к нам в филиал впервые приехал мой будущий научный руководитель и провел нам великолепный курс по теории графов. Меня так увлекла его манера преподавания, и тема была настолько интересна, что я не задумываясь после окончания курса а курсы от приезжих специалистов читались нам в сжатые сроки, примерно за месяц обратился с просьбой взять надо мной шефство.






На этом шаге мы рассмотрим раскраски графов. Вершинной раскраской далее - просто раскраской графа называется отображение множества вершин графа на конечное множество множество цветов ; n- раскраска графа - раскраска с использованием n цветов. Раскраска называется правильной, если никакие две вершины одного цвета не смежны.
- Дробная раскраска — это тема молодой области теории графов , известной как теория дробных графов.
- При решении практических задач с применением графов возникает необходимость в разбиении множества вершин графа на классы попарно несмежных между вершин.
- Вводим понятие списочной раскраски. Демонстрируем различие между обчным и списочным хроматическим числом.
- В задачах теории Рамсея часто рассматривают различные способы раскрашивания элементов некоторого множества например, чисел, рёбер графа и т.
- Все знают о задаче о четырех красках, но — до определенного предела. Позвольте пролить немного больше света.
- Доктор физико-математических наук, профессор, Дагестанский государственный университет. Asratyan и C.
- Теорема о четырёх красках утверждает, что всякую расположенную на плоскости или на сфере карту можно раскрасить не более чем четырьмя разными цветами красками так, чтобы любые две области с общим участком границы имели разный цвет.
- Поиск Написать публикацию.
- В этом уроке мы разберем, что такое раскраска графов и как это относится к цифрам на вершинах. Также покажем примеры раскраски графов разных типов, так как в каждом случае этот процесс немного отличается.



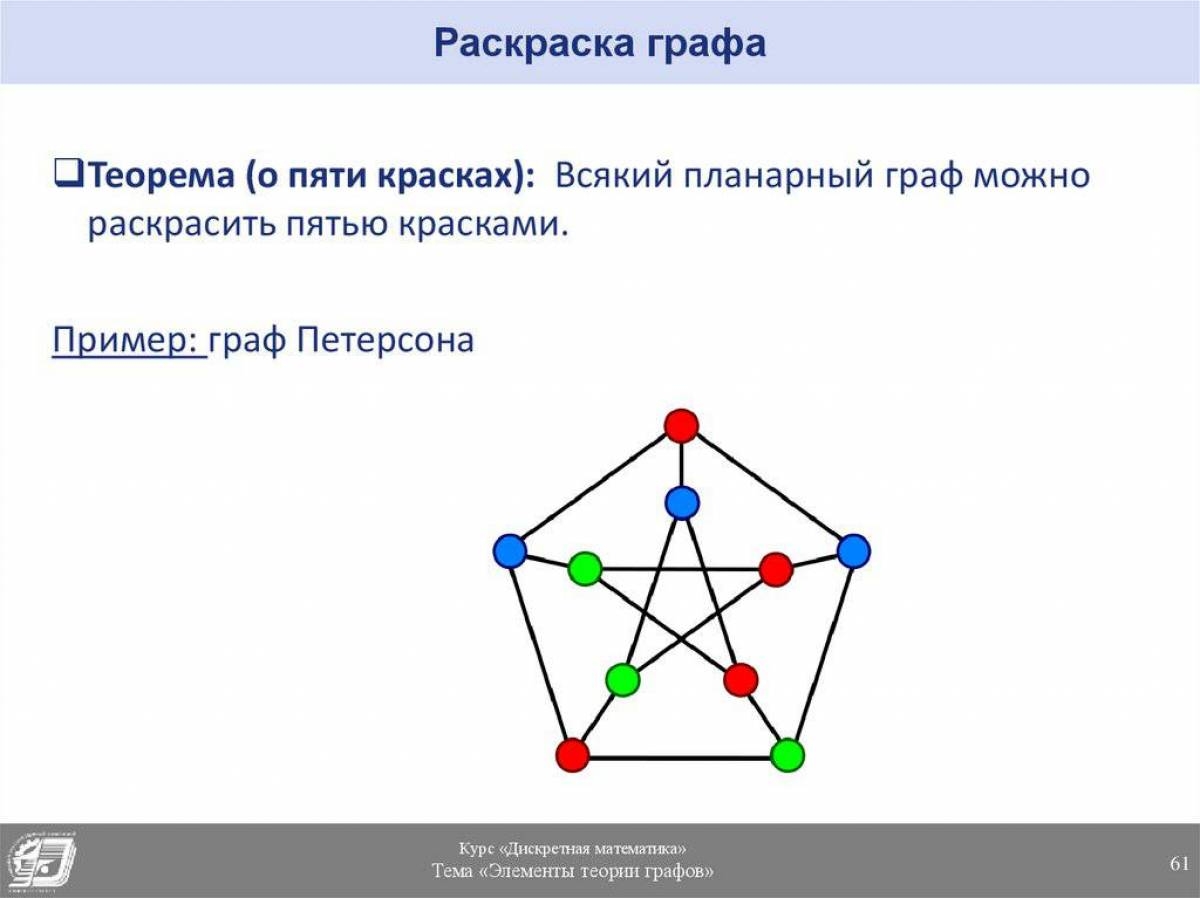



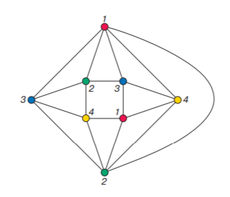


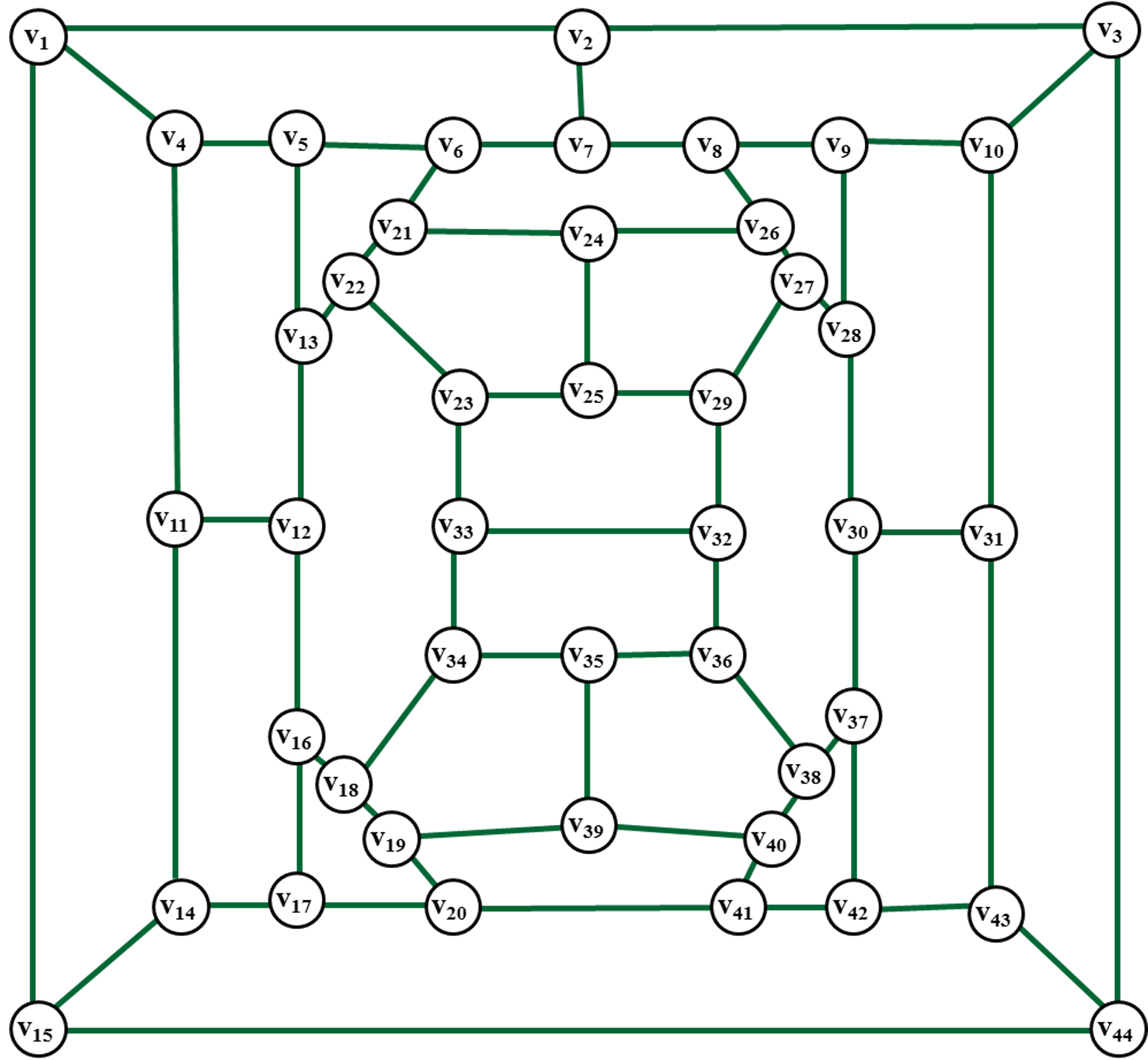
Теория Рамсея — раздел математики, изучающий условия, при которых в произвольно формируемых математических объектах обязан появиться некоторый порядок. Несложно доказать, что данные определения эквивалентны. Довольно часто определение для чисел Рамсея дается через задачу "о друзьях и незнакомцах" [1]. Чтобы получить лучшее представление природы чисел Рамсея, приведем пример. Такая раскраска представлена на рисунке справа.